 Teorema Wilson
Teorema Wilson
Jika p adalah bilangan prima maka

******************************************************
contoh soal:
Berapakah sisa

jika dibagi

?
jawab:
dengan teorema wilson didapat

INEQUALITY
AM-GM-HM
AM (Aritmatik Mean) yaitu rataan aritmatik.
Bentuk:

GM (Geometric Mean) yaitu rataan geometri.
Bentuk:
![\sqrt[n]{a_1 \times a_2 \times... \times a_n} \sqrt[n]{a_1 \times a_2 \times... \times a_n}](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_s7_3mE2HjDtP3bsU0qh5TeMsnsABe0VD1OPFKsfryaRrIXOxFs4boBD0GKWXJFzq0AiTMBWyUshRWOAJisxGHjwJHcd0UhGzctT6b-mt92JZjm3oQ3POoTQB3om8OFKVoojQcvGXEdZutGvEMiWDqWVu4jC8w8a7Jz-lwMQCmV-iaPvrKE-MedRmsXH2f7zk0N756VeW2j78vo=s0-d)
HM (Harmonik Mean) yaitu rataan harmonik.
Bentuk:

Untuk semua

bilangan real positif selalu berlaku

Contoh:
![\frac{1+2+3+4}{4} \ge \sqrt[4]{1 \times 2 \times 3 \times 4} \ge \frac{4}{\frac{1}{1}+ \frac{1}{2}+ \frac{1}{3}+ \frac{1}{5}} \frac{1+2+3+4}{4} \ge \sqrt[4]{1 \times 2 \times 3 \times 4} \ge \frac{4}{\frac{1}{1}+ \frac{1}{2}+ \frac{1}{3}+ \frac{1}{5}}](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vn6LWPt4S7MJeGmmSJjQi0_e7WSbfogjVoeYEFSvjpznLs4UYrDEJWDtbtQDjKWA1ugC8wmvREuHpFFgNcopWZhIVGPwT0OwwUVEk9RwwLBXHz3mewb0peDWs9fVocRmd-UYRnS-Osgi7JSfN1dvY-UnXlvO2hRdzHqZe8wZ-gUf_zqh5kmydcdJ_4qBPyu-Vb-qD_TYXzH1NT8yz4olFj9NJGGNI-xa7UTwQUbP_WSV5_yEoDF4wWetNofWm796DYJ4SUnnTlqhbbcQFStrfWurbcLHGqMzhjWUj1aFl74bAcz0rrIIRCybGEYJ4ZK3EEqm6ExV3-6ga2HJBP3jUxUpbdNy2rHsQBSzzcuCHBTcb9cJrZVAYdLBe7_-rlo4puTkyVVPBW_Bb2ZbTIcnFDPaDuO7z48Q=s0-d) CAUCHY_SCHWARZ
CAUCHY_SCHWARZ

CAUCHY_SWARCHZ BENTUK ENGEL

dimana 
atau jika dijabarkan menjadi

KETAKSAMAAN HOLDER
Misalkan

adalah bilangan real tidak negatif dan

. Maka

KETAKSAMAAN NESBITT
untuk

real positif berlaku

Chinese Remainder Theorem
Diberikan sistem kongruensi sebagai berikut.

haruslah saling relatif prima
Dengan demikian, kita dapat mencari nilai

dengan rumus berikut.
dimana


untuk setiap

.
dan

adalah invers dari

modulo

untuk setiap

.
———————————————————————————————————-
contoh:
Suatu bilangan bulat positif akan bersisa 1 jika dibagi 3, bersisa 2
jika dibagi 5, dan bersisa 3 jika dibagi 7. Tentukan bilangan bulat
terkecil yang memenuhi kondisi tersebut.


Karena 3,5, dan 7 relatif prima, maka rumus CRT (Chinese Remainder Theorem) dapat langsung digunakan.
Kita dapatkan

,

,

, dan
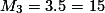
. Untuk menentukan

, kita selesaikan

, menjadi

, maka

. Untuk menentukan

, kita selesaikan

, maka

. Untuk menentukan

, kita selesaikan
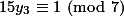
, maka

Tinggal memasukkan semua elemen yang ada ke dalam rumus


Jadi, bilangan yang dimaksud adalah 52.
Fermat’s Little Theorem
Fermat’s Little Theorem
Jika

adalah bilangan prima dan

adalah integer positif dimana

,maka

—————————————————————————————————————————–
Fermat’s Little Theorem (bentuk lain)
Jika

adalah bilangan prima dan

adalah integer positif, maka
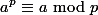
Note: perhatikan bahwa

bukanlah syarat wajib.
——————————————————————————————————————————–
contoh:
Tentukan sisa pembagian jika

dibagi 73.
Jawab:
73 adalah bilangan prima, maka dari Fermat’s Little Theorem kita tahu bahwa

.
Maka, kita kelompokkan berdasarkan 72.







.
Selanjutnya, kita gunakan cara biasa.





___________

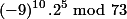


___________




___________




___________


___________




___________


.
Jadi, sisa pembagiannya adalah 32.
Euler Phi Function
Euler Phi-Function digunakan dalam teorema Euler. Meskipun namanya
menggunakan kata phi namun fungsi ini sama sekali tidak menggunakan nila

. Penggunaan phi semata-mata untuk “fungsi”
Euler phi function  adalah fungsi yang menghitung banyaknya bilangan bulat
adalah fungsi yang menghitung banyaknya bilangan bulat  yang koprima dengan
yang koprima dengan 
contoh

Karena dari sepuluh bilangan kurang dari atau sama dengan 10: 1,2,3,4,5,6,7,8,9,10
terdapat 4 bilangan yang koprima dengan 10 yaitu 1,3,7,9

Berikut adalah teorema-teorema yang perlu diperhatikan dalam Euler Phi-Function:
Teorema Pertama
Untuk n bilangan prima, selalu berlaku 
Contoh:

******
Teorema Kedua
Untuk

bilangan prima dan

bilangan bulat positif, selalu berlaku
 atau ekuivalen dengan
atau ekuivalen dengan 
contoh

*******
Teorema Ketiga
Phi function adalah fungsi multiplikatif.
Untuk m dan n saling relatif prima (koprima), maka

contoh

******
Kalau repot dengan seluruh rumus diatas, pakai saja konsep di bawah

merupakan faktorisasi prima dari bilangan bulat n, maka

contoh

*******
Ingat bahwa  selalu bernilai genap untuk
selalu bernilai genap untuk 
Teorema Euler
Fermat’s Little Theorem (FLT) akan
sangat bermanfaat jika bilangannya adalah bilangan prima. Masalahnya,
bagaimana kalau bilangannya komposit?
Leonhard Euler berhasil membuktikan FLT
pada tahun 1736. Kemudian, 24 tahun kemudian, FLT digeneralisasi oleh
Generalisasi inilah yang disebut sebagai Teorema Euler.
Teorema Euler
Untuk  adalah integer positif dan
adalah integer positif dan  adalah integer dimana
adalah integer dimana  , maka
, maka

Jika, m adalah bilangan prima, maka rumus di atas akan identik dengan FLT
CONTOH
Berapakah sisa pembagian jika  dibagi 35
Solusi:
Berdasarkan teorema euler
dibagi 35
Solusi:
Berdasarkan teorema euler
 Maka pangkatnya kita kelompokan berdasarkan 24
Maka pangkatnya kita kelompokan berdasarkan 24
 Dengan begitu dapat dengan mudah diselesaikan. Hingga akhirnya didapat
Dengan begitu dapat dengan mudah diselesaikan. Hingga akhirnya didapat

jadi, sisanya adalah 11
Bukti Teorema Ceva

Jika D,E,F berturut-turut merupakan titik-titik pada garis BC,CA,AB pada

, maka:
Garis BE,AD,FC berpotongan di satu titik jika dan hanya jika
Untuk membuktikan teorema di atas maka akan kita bagi menjadi dua kasus:
1. Jika BE,AD,FC berpotongan di satu titik maka

Sifat segitiga: Perbandingan luas segitiga yang tingginya sama, sama dengan perbandingan panjang alas-alasnya.
Berdasarkan sifat di atas didapatkan:
(ket: AFC maksudnya adalah luas

)
Dengan cara serupa didapatkan:
Jadi, diperoleh

Terbukti
2. Jika

maka BE,AD,FC kongruen.
Untuk membuktikannya, sebenarnya cukup
sederhana. Misalkan BE dan AD berpotongan di O dan perpanjangan CO
memotong AB di G. Maka menurut torema ceva (no.1), didapatkan

Sebelumnya juga telah diketahui bahwa

, maka jelas bahwa F dan G berimpit. Jelas terbukti bahwa ketiga garis tadi berpotongan di satu titik.
(contoh ini sama sekali tidak menggunakan teorema ceva itu sendiri.
Namun konsep yang digunakan adalah konsep yang terdapat dalam pembuktian
dari teorema ceva. Ingat bahwa, bukti dari suatu rumus lebih berari
dari rumus itu sendiri)
D, E, dan F adalah titik-titik pada sisi BC, CA, AB dari segitiga ABC
dan AD, BE, dan CF kongruen terhadap titik O. Buktikan bahwa

Solusi:
Penampakan soal tersebut kurang lebih seperti ini:
Berdasarkan sifat segitiga yang tercantum jauh di atas, didapat:

Dengan proses serupa didapatkan pula

dan

Dari ketiga persamaan tersebut, maka
bahwa

[OSP 2010] Diketahui segitiga

dengan panjang sisi-sisinya adalah

. Jika

, tentukan besar sudut yang mengahap sisi

.
Solusi:

. Dengan rumus kosinus,

, maka

Kembali ke soal maka

, sehingga

Bagi kedua ruas dengan

. didapat

.Jadi besar sudut C adalah

Koefisien Ekspansi
Berapakah koefisien

pada ekspansi

Solusi:




.
.
.

Jadi, koefisien

adalah -1005








 haruslah saling relatif prima
haruslah saling relatif prima dengan rumus berikut.
dengan rumus berikut.

 untuk setiap
untuk setiap  .
. adalah invers dari
adalah invers dari  modulo
modulo  untuk setiap
untuk setiap 


 ,
,  ,
,  , dan
, dan 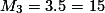 . Untuk menentukan
. Untuk menentukan  , kita selesaikan
, kita selesaikan  , menjadi
, menjadi  , maka
, maka  . Untuk menentukan
. Untuk menentukan  , kita selesaikan
, kita selesaikan  , maka
, maka  . Untuk menentukan
. Untuk menentukan  , kita selesaikan
, kita selesaikan 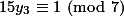 , maka
, maka 


 adalah bilangan prima dan
adalah bilangan prima dan  adalah integer positif dimana
adalah integer positif dimana  ,maka
,maka 
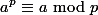
 dibagi 73.
dibagi 73. .
.


 .
.

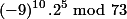








 .
.